 |
G+Smo
24.08.0
Geometry + Simulation Modules
|
|
|
G+Smo
24.08.0
Geometry + Simulation Modules
|
|
A class for computing periodic parametrizations of closed (cylinder-like) surface meshes. The result will be periodic in the u-direction and the parameter domain will be [0, 1]^2. This class is an alternative to gsPeriodicOverlap. The idea is adapted from
Tong, Y., Alliez, P., Cohen-Steiner, D., Desbrun, M.: Designing quadrangulations with discrete harmonic forms, in: Sheffer, A., Polthier, K. (Eds.), Symposium on Geometry Processing, Eurographics. pp. 201–210, 2006,
where it was used constructing discrete harmonic mappings on arbitrary topology.
The user prescribes the u-values of the points on the lower and upper boundaries (i.e., v = 0 and v = 1, respectively). In addition, they are required to provide a stitch: a list of vertices forming a simple polyline connecting the vertices with the highest u-value on v=0 and v=1, which serves as a first guess for the location of the periodic interface.
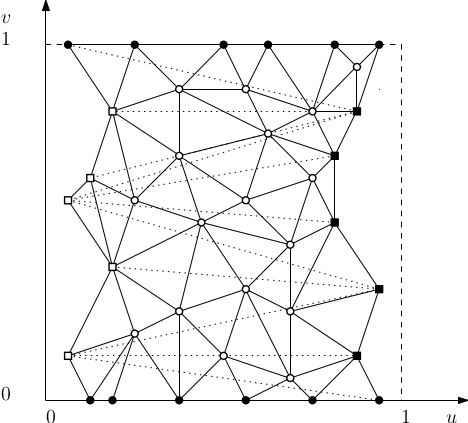
The equations for the inner vertices (depicted with empty circles in the figure below) are assembled by the methods of the parent class. For vertices on the stitch (full squares) the u-coordinate of their neighbours to the right (empty squares) is temporarily increased by one; similarly, when computing the empty-squared neighbours, the u-coordinate from the full-square neighbours is decreased by one.
Inherits gsPeriodicParametrization< T >.
Collaboration diagram for gsPeriodicStitch< T >:Classes | |
| class | Neighbourhood |
Public Member Functions | |
| void | compute () |
| Computes the periodic parametrization. | |
| gsMesh< T > | createFlatMesh () const |
| gsMatrix< T > | createUVmatrix () |
| gsMatrix< T > | createXYZmatrix () |
| gsPeriodicStitch (const gsMesh< T > &mesh, const gsMatrix< T > &verticesV0, const gsMatrix< T > ¶msV0, const gsMatrix< T > &verticesV1, const gsMatrix< T > ¶msV1, const gsMatrix< T > &stitchVertices, const gsOptionList &list=gsParametrization< T >::defaultOptions()) | |
| void | restrictMatrices (gsMatrix< T > &uv, const gsMatrix< T > &xyz, real_t uMin=0, real_t uMax=1) const |
| void | writeTexturedMesh (std::string filename) const |
Static Public Member Functions | |
| static gsOptionList | defaultOptions () |
| Returns the list of default options for gsParametrization. | |
Protected Member Functions | |
| void | calculate (const size_t paraMethod) |
| void | constructAndSolveEquationSystem (const Neighbourhood &neighbourhood, const size_t n, const size_t N) |
| void | constructAndSolveEquationSystem (const Neighbourhood &neighbourhood, const size_t n, const size_t N) |
| Constructs linear equation system and solves it. More... | |
| gsMesh< T > | createUnfoldedFlatMesh () const |
| bool | edgeIsInCorrections (index_t beg, index_t end) const |
| const Point2D & | getParameterPoint (size_t vertexIndex) const |
| Get parameter point Returns the parameter point with given vertex index. More... | |
| void | initParameterPoints () |
| bool | isOnStitch (size_t vertexIndex) const |
Protected Attributes | |
| gsSparseMatrix< int > | m_corrections |
| const std::vector< size_t > | m_indicesV0 |
| indices of the vertices with v=0 | |
| const std::vector< size_t > | m_indicesV1 |
| indicesV1 indices of the vertices with v=1 | |
| const gsHalfEdgeMesh< T > | m_mesh |
| mesh information | |
| VectorType | m_parameterPoints |
| parameter points | |
| const gsMatrix< T > | m_paramsV0 |
| u-parameters of the vertices with v=0 | |
| const gsMatrix< T > | m_paramsV1 |
| u-parameters of the vertices with v=1 | |
| const std::vector< size_t > | m_stitchIndices |
| indices of the vertices on the stitch | |
|
inlineexplicit |
Constructor
| mesh | the surface mesh to be parametrized |
| verticesV0 | matrix with three rows containing the vertices with v=0 |
| paramsV0 | matrix with one row containing the u-parameters of vertices with v=0 |
| verticesV1 | matrix with three rows containing the vertices with v=1 |
| paramsV1 | matrix with one row containing the u-parameters of vertices with v=1 |
| stitchVertices | matrix with three rows containing the vertices on the stitch |
| list | list of the method options |
|
protected |
Calculation itself
| paraMethod | parametrization method (cf. gsParametrization<T>) |
Solve.
|
protected |
Similar to constructAndSolveEquationSystem but works for periodic meshes using the corrections.
|
protectedinherited |
Constructs linear equation system and solves it.
The last step in Floater's algorithm is solving the linear equation system to obtain the parameter values for the inner vertices of the triangle mesh. This method constructs the above-mentioned system using information from neighbourhood. The matrix is given by a(i,i) = 1 a(i,j) = -lambda(i,j) for j!=i and the right hand side is calculated using the boundary parameters found beforehand. The parameter values are multiplied with corresponding lambda values and summed up. In the last step the system is solved and the parameter points are stored in m_parameterPoints.
| [in] | neighbourhood | const Neighbourhood& - neighbourhood information of the mesh |
| [in] | n | const int - number of inner vertices and therefore size of the square matrix |
| [in] | N | const int - number of the vertices and therefore N-n is the size of the right-hand-side vector |
|
inlinevirtual |
Creates a flat mesh out of a periodic parametrization created by a the stitch method. The mesh is then restricted to [0, 1]^2.
Reimplemented from gsParametrization< T >.
|
protected |
Creates an unfolded mesh in the sense that the vertices on the stitch are present twice, once in their original parameters and once with u decreased by one.
|
inherited |
Parametric Coordinates u,v from 0..1
|
inherited |
Corresponding mapped values in R3 to parametric coordinates.
Query, whether an edge between vertices with indices beg and end corrects a stitch vertex with its neighbour to the right (i.e., whether it connects and empty square and full square vertex in the figure documenting this class).
|
protectedinherited |
Get parameter point Returns the parameter point with given vertex index.
| [in] | vertexIndex | int - vertex index |
|
protectedinherited |
Prepares m_parameterPoints for a computation of a periodic parametrization. Important: Neighbourhood has to be constructed before calling this function.
|
inlineprotected |
Query, whether the vertex with index vertexIndex (in the numbering of Floater's paper, i.e., starting from 1) is on the stitch or not.
|
inherited |
Moves the u-coordinates of parameters outside the interval [uMin, uMax] to inside the interval. Note: it modifies uv!
| uv | Matrix of the parameters, one column per point |
| xyz | Matrix of the coordinates, one column per point |
| uMin | minimal desired u |
| uMax | maximal desired u |
|
inherited |
Writes m_mesh into filename.vtk with the vertices coloured according to the parameters.
| filename | The name of the output file (without extension). |
|
protected |
Slot (i, j) is equal to 1 iff vertex with id i-1 is on a stitch and vertex with id j-1 is among its neighbours across the interface. Slot (j, i) is then set to -1.
