Detailed Description

This module contains the B-spline and NURBS basis functions.

G+Smo is very powerful in dealing with tensor-product B-splines:

A tensor B-spline basis.

Evaluation of B-splines

There are several functions with similar names. The following table should help you in find the proper one for you.

Name of procedure	Which basis function	Evaluate what
`eval(u)`	all active at u	value
`evalSingle(i, u)`	basis function i	value
`deriv(u)`	all active at u	first derivative(s)
`derivSingle(i, u)`	basis function i	first derivative(s)
`deriv2(u)`	all active at u	second derivative(s)
`deriv2Single(i, u)`	basis function i	second derivative(s)
`evalAllDers(u, k)`	all active at u	value and all derivatives up to order k
`evalAllDersSingle(i,u,k)`	basis function i	value and all derivatives up to order k
`evalDerSingle(i, u, k)`	basis function i	k-th derivative (k=0, ... , p-1)

Here u is a matrix of values, and every column corresponds to one evaluation point.

All the above functions return a unique pointer. Also, for each of these functions there is a variant suffixed with _into, for example eval_into, deriv2Single_into, and so on, that returns void, takes an additional matrix result as argument, and writes the result in that matrix.

One of the lovely things about G+Smo is that it in works nicely in arbitrary dimension and the functions look virtually the same. So if you work with a tensor-product basis, your matrix u has to have exactly as many rows as the number of variables and then it is used the same way as in the univariate case.

The price you pay for arbitrary dimension is that the results are returned in a somehow magical manner. That is, every column of result then contains values of active functions in ascending order. Thus it is usually used together with active_into. See the following example.

Example of evaluation

We create a bivariate quadratic tensor-product basis and evaluate the basis functions in several points. First, we need knot vectors:

gsKnotVector<> kv0(0,1,1,3); //start, end, interior knots, multiplicities of start/end knots
gsKnotVector<> kv1(0,1,1,3);

The Greville abscissae are 0, 0.25, 0.75 and 1.

Todo:: Check these numbers; correct or update picture?

Then we create the basis by

gsTensorBSplineBasis<2,double> tbas (new gsBSplineBasis< double >(kv0), new gsBSplineBasis< double >(kv1));

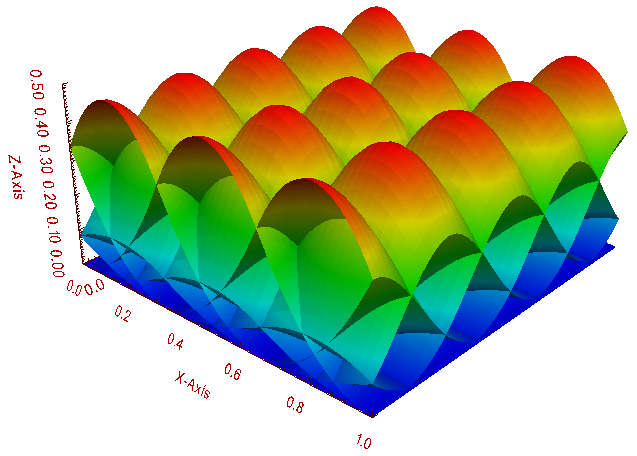
Now we have 16 basis functions, the following figure shows them together with the points where we are going to evaluate them.

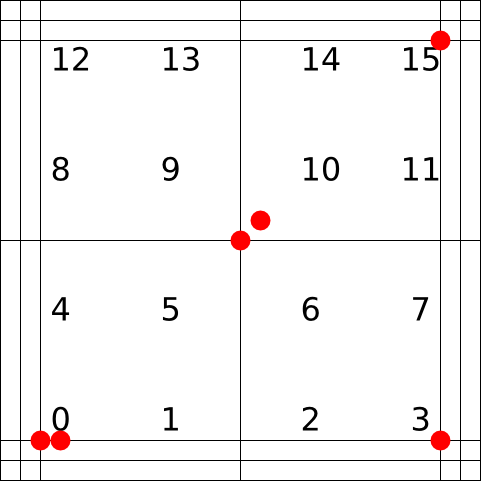
Mesh, numbers correspond to Greville abscissae of the basis functions, red dots to evaluation points.

We prepare six evaluation points (0,0), (0.1,0), (1,0), (0.5,0.5), (0.6,0.6), (1,1) by

gsMatrix< double > uVals(2,6);
uVals << 0,0.1,1,0.5,0.6,1, 0,0,0,0.5,0.6,1;

and the matrices for results by

gsMatrix< unsigned > actRes;
gsMatrix< double > valRes;

Note: Note that actRes requires a matrix of unsigned, otherwise you obtain a hardly comprehensible error. This situation is good to remember in similar cases.

Now we ask for the evaluation and printing of the results

tbas.active_into(uVals,actRes);
tbas.eval_into(uVals,valRes);
std::cout << "Active functions:\n" << actRes << "\n\nResults of evaluation:\n" << valRes << "\n";

You should obtain something like

Active functions:
 0  0  1  5  5  5
 1  1  2  6  6  6
 2  2  3  7  7  7
 4  4  5  9  9  9
 5  5  6 10 10 10
 6  6  7 11 11 11
 8  8  9 13 13 13
 9  9 10 14 14 14
10 10 11 15 15 15

Results of evaluation:
     1   0.64      0   0.25 0.1024      0
     0   0.34      0   0.25 0.2048      0
     0   0.02      1      0 0.0128      0
     0      0      0   0.25 0.2048      0
     0      0      0   0.25 0.4096      0
     0      0      0      0 0.0256      0
     0      0      0      0 0.0128      0
     0      0      0      0 0.0256      0
     0      0      0      0 0.0016      1

From the first matrix we may read that the active functions in (0,0) are functions number 0, 1, 2, 4, 5, 6, 8, 9, 10 (check with the figure). Similarly, the second column shows us the basis functions active in (0.1, 0) etc.

In the second matrix we see the actual values. The first column tells us that there is just one active function in (0,0) and is equal to 1 there. In (0.1, 0) we have more active functions; value of the 0th is equal to 0.64, 1th to 0.34, 2nd to 0.02 and the others are equal to zero (don't worry about that, the evaluation point is at the border of their supports). Interesting is the fourth column: we may see that in the middle of the domain there are four nonzero functions, their indices are 5, 6, 9 and 10 and all the values are equal to 0.25.

Note: You may observe the partition of unity. The sum of all the entries in each column should be equal to one.

Evaluation of derivatives goes along similar lines and we invite you to play around with them in your test file.

Namespaces
	gismo::bspline
	This namespace contains implementation of B-spline related algorithms.

Classes
class	gsBSpline< T >
	A B-spline function of one argument, with arbitrary target dimension. More...

class	gsBSplineBasis< T >
	A univariate B-spline basis. More...

class	gsNurbs< T >
	A NURBS function of one argument, with arbitrary target dimension. More...

class	gsNurbsBasis< T >
	A univariate NURBS basis. More...

struct	gsNurbsCreator< T >
	Class gsNurbsCreator provides some simple examples of Nurbs Geometries. More...

struct	gsPanelCreator< T >
	Class gsPanelCreator provides some simple examples of Nurbs Geometries. More...

class	gsTensorBSpline< d, T >
	A tensor product of d B-spline functions, with arbitrary target dimension. More...

class	gsTensorBSplineBasis< d, T >
	A tensor product B-spline basis. More...

class	gsTensorBSplineBasis< 1, T >
	A univariate B-spline basis. More...

class	gsTensorNurbs< d, T >
	A tensor product Non-Uniform Rational B-spline function (NURBS) of parametric dimension d, with arbitrary target dimension. More...

class	gsTensorNurbsBasis< d, T >
	A tensor product Non-Uniform Rational B-spline (NURBS) basis. More...

Functions
template<typename T >
unsigned	findHyperPlaneIntersections (const gsBSpline< T > &curve, const gsVector< T > &normal, T reference, T tolerance, std::vector< Root< T > > &roots)
	find intersections of a BSpline curve with an hyperplane More...

	gsBSpline (T u0, T u1, unsigned interior, int degree, gsMatrix< T > coefs, unsigned mult_interior=1, bool periodic=false)
	Construct a B-spline from an interval and knot vector specification. More...

template<typename T , typename KnotVectorType , typename Mat >
void	gsTensorBoehm (KnotVectorType &knots, Mat &coefs, T val, int direction, gsVector< unsigned > str, int r=1, bool update_knots=true)

template<typename KnotVectorType , typename Mat , typename ValIt >
void	gsTensorBoehmRefine (KnotVectorType &knots, Mat &coefs, int direction, gsVector< unsigned > str, ValIt valBegin, ValIt valEnd, bool update_knots=true)

template<short_t d, typename KnotVectorType , typename Mat , typename ValIt >
void	gsTensorBoehmRefineLocal (KnotVectorType &knots, const unsigned index, Mat &coefs, gsVector< index_t, d > &nmb_of_coefs, const gsVector< index_t, d > &act_size_of_coefs, const gsVector< index_t, d > &size_of_coefs, const unsigned direction, ValIt valBegin, ValIt valEnd, const bool update_knots)
	Local refinement algorithm. More...

template<short_t d, typename T , typename KnotVectorType , typename Mat >
void	gsTensorInsertKnotDegreeTimes (const KnotVectorType &knots, Mat &coefs, const gsVector< index_t, d > &size_of_coefs, T val, const unsigned direction, gsVector< index_t, d > &start, gsVector< index_t, d > &end)
	Inserts knot val such that multiplicity of a val in knot vector is equal degree. More...

void	refine (gsMatrix< T > const &boxes, int refExt=0)
	Refinement of the tensor basis on the area defined by boxes. More...

Function Documentation

unsigned findHyperPlaneIntersections	(	const gsBSpline< T > &	curve,
		const gsVector< T > &	normal,
		T	reference,
		T	tolerance,
		std::vector< Root< T > > &	roots
	)

find intersections of a BSpline curve with an hyperplane

This function tries to be robust and to report correctly intersections of the curve with the given hyperplane of thickness 2*tolerance. Intersections are roots of a B-Spline curve and they can be of four types:

-odd points, i.e. the position with respect to the hyperplane changes at the intersection

-even points, i.e. the position with respect to the hyperplane is the same before and after the intersection

-odd intervals, i.e. the curve stays for a full parametric interval in the hyperplane and then exit on the other side of it

-even intervals, i.e. the curve stays for a full parametric interval in the hyperplane and then exit on the side it comes from

The intersections are reported as encountered while following the curve in the direction given by increasing parameter.

This function assumes an open knot vector: the first and last control points are in the curve. If the start or the end of the the curve is on the hyperplane it is reported as an odd intersection. This means that this special case must be handled outside of this function when used to determine if a point is inside a 2D area bounded by a closed curve.

gsBSpline	(	T	u0,
		T	u1,
		unsigned	interior,
		int	degree,
		gsMatrix< T >	coefs,
		unsigned	mult_interior = `1`,
		bool	periodic = `false`
	)

inline

Construct a B-spline from an interval and knot vector specification.

Parameters

u0	starting parameter
u1	end parameter
interior	number of interior knots
degree	degree of the spline space
coefs	coefficients of the spline space
mult_interior	multiplicity at the interior knots
periodic	specifies whether the B-spline is periodic

void gsTensorBoehm	(	KnotVectorType &	knots,
		Mat &	coefs,
		T	val,
		int	direction,
		gsVector< unsigned >	str,
		int	r = `1`,
		bool	update_knots = `true`
	)

Performs a knot insertion on knots and recomputes coefficients.

Parameters

knots	- vector of knots in direction "direction"
coefs	- coefficients (control points)
val	- value of a knot we will insert
direction	- in which direction (knot vector) we will insert knot
str	- vector of strides
r	- how many times we will insert knot
update_knots	- if we update knots or not

void gsTensorBoehmRefine	(	KnotVectorType &	knots,
		Mat &	coefs,
		int	direction,
		gsVector< unsigned >	str,
		ValIt	valBegin,
		ValIt	valEnd,
		bool	update_knots = `true`
	)

Performs a knot refinement and recomputes coefficients.

Parameters

knots	- knot vector in direction "direction"
coefs	- coefficients (control points)
direction	- in which direction we will refine knots
str	- vector of strides
valBegin	- iterator pointing to the begining of the vector of the knots we want to insert
valEnd	- iterator pointing to the end of the vector of the knots we want to insert
update_knots	- if we should update "knots" or not

void gsTensorBoehmRefineLocal	(	KnotVectorType &	knots,
		const unsigned	index,
		Mat &	coefs,
		gsVector< index_t, d > &	nmb_of_coefs,
		const gsVector< index_t, d > &	act_size_of_coefs,
		const gsVector< index_t, d > &	size_of_coefs,
		const unsigned	direction,
		ValIt	valBegin,
		ValIt	valEnd,
		const bool	update_knots
	)

Local refinement algorithm.

We refine given coefficients (coefs) in given direction with corresponding knots. Knots, we want to insert, can be accessed through iterators valBegin and valEnd. Index is index of the first basis function, in given direction, that corresponds to first coefficient in the coefs matrix. Through variable update_knots we can set if we want to add inserted knots into knot vector knots. Variables nmb_of_coefs, act_size_of_coefs and size_of_coefs describe coefs matrix.

We can use bigger coefs matrix than needed. Act_size_of_coefs describes actual size of the coefficients. (For example sizes of the edges of the cube that coefs matrix represents in 3D.) Size_of_coefs is size of the coefficients we will populate in this function call. Nmb_of_coefs presents number of nonzero coefficients in coefs matrix.

void gsTensorInsertKnotDegreeTimes	(	const KnotVectorType &	knots,
		Mat &	coefs,
		const gsVector< index_t, d > &	size_of_coefs,
		T	val,
		const unsigned	direction,
		gsVector< index_t, d > &	start,
		gsVector< index_t, d > &	end
	)

Inserts knot val such that multiplicity of a val in knot vector is equal degree.

Function inserts the knot val into knot vector knots, such that multiplicity of val becomes knots.degree(). Given coefficients coefs must be local to the knot val (coefficients corresponding to the active base functions at val). size_of_coefs are sizes of the coefficients. direction is direction in which we perform a knot insertion. Sometimes we dont need to insert a knots at all rows at direction. With variables start and end, we can set subcube of the coefs where we will perform a knot insertion.

This function should just be used for evaluation via knot insertion (not the full coefficient matrix will be computed).

void refine	(	gsMatrix< T > const &	boxes,
		int	refExt = `0`
	)

virtual

Refinement of the tensor basis on the area defined by boxes.

Applies "local" refinement within the tensor-product structure of gsTensorBSplineBasis. The areas for refinement are specified in boxes.
boxes is a gsMatrix of size d x (2*N), where
d is the dimension of the parameter domain and
N is the number of refinement boxes.

Every two successive columns in boxes correspond to the coordinates of the lower and upper corners of one refinement box, respectively (see example below). Note that a new knot will be inserted in every knot span contained in this area. If some of the given boxes overlap, the refinement will only be done once.

Example, let

d = 2
knotvector1 = knotvector2 = [ 0 0 0  0.25  0.5  0.75  1 1 1 ]

boxes = [ 0.25  0.75  0     0.5 ]
[ 0     0.25  0.75  1   ]

The areas [ 0.25, 0.75 ] x [ 0, 0.25 ] and [ 0, 0.5 ] x [ 0.75, 1 ] will be refined. The knots 0.125, 0.375, and 0.625 will be inserted in knotvector1, and the knots 0.125 and 0.875 in knotvector2.

Parameters

[in]	boxes	gsMatrix of size d x (2N)*; specifies areas for refinement. See above for details and format.
[in]	refExt	is ignored

Remarks: NOTE This function directly modifies the basis (by inserting knots in the underlying univariate B-spline bases).

 \note: the \a refExt parameter is ignored in this implementation

Reimplemented from gsBasis< T >.

Detailed Description

Evaluation of B-splines

Example of evaluation

Namespaces

Classes

Functions

Function Documentation