 |
G+Smo
25.01.0
Geometry + Simulation Modules
|
 |
G+Smo
25.01.0
Geometry + Simulation Modules
|
This module implements hierarchical and truncated hierarchical tensor-product B-splines.
See also thbSplineBasis_example.cpp and adaptRefinementThb_example.cpp.
We will now have a closer look at the gsThbs_test.cpp file. After parsing the command line arguments it either reads the hierarchical basis from the file given by the user or runs a default example. To understand how the hierarchical basis is specified you can look into the file with the default example. This you do by
cat ./filedata/thbbasis/simple.xml
in your gismo-build directory. This should give something like
This means that we are first given a unit square equidistantly divided into 16 pieces and having triple knots on the boundary. Note number 2 in the specification of the THBSplineBasis2 (and the other bases as well) telling the number of variables. If omitted, it is expected to be one as in the case of the univariate bases in the tensor product. Note also that levels="3". This means that (in the current implementation) cannot get more than three levels of dyadic refinement.
This leads us to an important concept of local and global indices. Internally, G+Smo stores the knot points indexed by the finest level. See the following table.
| physical coordinates | 0 | 0.25 | 0.5 | 0.75 | 1 |
|---|---|---|---|---|---|
| indices in level 0 | 0 | 1 | 2 | 3 | 4 |
| indices in level 1 | 0 | 2 | 4 | 6 | 8 |
| indices in level 2 | 0 | 4 | 8 | 12 | 16 |
The mesh is then refined in the specified boxes. Important is that each of these boxes is specified by its lower left and upper right corner and these corners are given in the indices of the current level. The final mesh together with the bivariate (check, where this is specified!) basis functions is depicted in Figure 1.
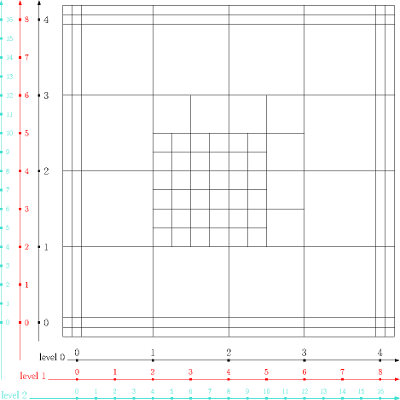
The triple knots at the domain boundary are shown with spaces for illustration. First we refined the square \( [2,6]\times [2,6]\) in the numbering of level 1 and then the square \( [4,10]\times [4,10]\) in the indices of level 2. The physical coordinates are visible from the picture.
The active basis functions (those that are in the hierarchical basis) are printed in the console as the output of gsThbs_test.cpp starting with
Characteristic matrix:
There should be 36, 3 and 16 basis functions in levels 0, 1 and 2, respectively. The basis functions are given as pairs \((x,y)\), where \(x\) is the number of this basis function in the horizontal direction counted from the left (note that the functions in each level has their own numbering, since the size of their support is different) and \(y\) is its number in the vertical numbering starting from below. Consult Figure 2 for the numbering of the basis functions.
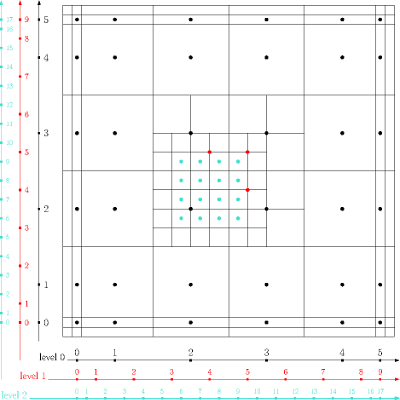
You can see the mesh specified in ~gismo/filedata/thbbasis/simple.xml together with the Greville points (center points of supports) of the basis functions. Basis functions from levels 0, 1 and 2 are marked by black, red and turqoise dots, respectively. The axes show the numbering of the basis functions from the three levels.
Classes | |
| struct | gsAABB< d, Z > |
| Struct of for an Axis-aligned bounding box. More... | |
| class | gsHBox< d, T > |
| This class provides a Hierarchical Box (gsHBox) More... | |
| class | gsHBSpline< d, T > |
| A hierarchical B-Spline function, in d dimensions. More... | |
| class | gsHBSplineBasis< d, T > |
| A hierarchical B-spline basis of parametric dimension d. More... | |
| class | gsHDomain< d, Z > |
| Class with a hierarchical domain structure represented by a box k-d-tree. More... | |
| class | gsHDomainBoundaryIterator< T, d > |
| Re-implements gsDomainIterator for iteration over all boundary elements of a hierarchical parameter domain. More... | |
| class | gsHDomainIterator< T, d > |
| Re-implements gsDomainIterator for iteration over all boundary elements of a hierarchical parameter domain. More... | |
| class | gsHDomainLeafIter< node, isconst > |
| Iterates over the leaves of an gsHDomain (tree). More... | |
| class | gsHDomainSliceIter< node, isconst > |
| Iterates over the leaves of an gsHDomain (tree) that intersect with a slice position. More... | |
| class | gsHFitting< d, T > |
| This class applies hierarchical fitting of parametrized point clouds. More... | |
| class | gsHTensorBasis< d, T > |
| Class representing a (scalar) hierarchical tensor basis of functions \( \mathbb R^d \to \mathbb R \). More... | |
| struct | gsKdNode< d, Z > |
| Struct representing a kd-tree node. More... | |
| class | gsRationalTHBSpline< d, T > |
| A rational truncated hierarchical B-Spline function of parametric dimension d, with arbitrary target dimension. More... | |
| class | gsRationalTHBSplineBasis< d, T > |
| A rational Truncated Hierarchical B-Spline basis. More... | |
| class | gsTHBSpline< d, T > |
| A truncated hierarchical B-Spline function, in d dimensions. More... | |
| class | gsTHBSplineBasis< d, T > |
| Truncated hierarchical B-spline basis. More... | |
| class | gsVSegment< T > |
| Class for representing a vertical line segment in 2D. Helper for the class gsAAPolyline. More... | |