Tutorial 02: Geometry

In this tutorial you will get to know the main geometric objects and operations available in the library. Since all parametric curves, surfaces or volumes are geometric objects, all these derive from gsGeometry, which in turn derives from gsFunction.

Univariate B-splines

• gsKnotVector The main ingredient for constructing a B-spline basis is a knot vector. See knotVector_example.cpp.

• gsBSplineBasis

  This class derives from gsBasis, representing a set of B-spline basis functions. These are polynomial functions, i.e. there are no weights (the weights if we regard them as NURBS are all equal to 1, therefore not stored).
  

  Here is an example of how to create a knot vector and a B-spline basis, followed by uniform refinement.

  #include <gismo.h>
   
  using namespace gismo;
   
  int main(int, char**)
  {
      gsKnotVector<>   kv (-1, 0, 3, 3, 1 );
      gsBSplineBasis<> basis(kv);
      gsInfo << basis.detail() << "\n";
   
      basis.uniformRefine();
      gsInfo << basis.detail() << "\n";
   
      return 0;
  }

  Output:

  BSplineBasis: deg=2, size=6, knot vector:
  [ -1 -0.75 -0.5 -0.25 0 ] ~ ( 3 1 1 1 3 )
  deg=2, size=9, uSize=5, minSpan=0.25, maxSpan=0.25
  
  BSplineBasis: deg=2, size=10, knot vector:
  [ -1 -0.875 -0.75 -0.625 -0.5 -0.375 -0.25 -0.125 0 ] ~ ( 3 1 1 1 1 1 1 1 3 )
  deg=2, size=13, uSize=9, minSpan=0.125, maxSpan=0.125
  
  

  Here is an example of how to get basis functions active on one point, and their corresponding values.

  #include <gismo.h>
   
  using namespace gismo;
   
  int main(int, char**)
  {
      gsKnotVector<>   kv (-1, 0, 3, 3, 1 );
      gsBSplineBasis<> basis(kv);
      gsInfo << basis.detail() << "\n";
   
      gsMatrix<> pt(1,1);
      pt << 0;
   
      gsMatrix<index_t> act;
      gsMatrix<> val;
      basis.active_into(pt, act);
      basis.eval_into(pt, val);
      gsInfo << "Active basis functions on " << pt << ":\n" << act << "\n";
      gsInfo << "And their values:\n" << val << "\n";
      return 0;
  }

  Output:

  BSplineBasis: deg=2, size=6, knot vector:
  [ -1 -0.75 -0.5 -0.25 0 ] ~ ( 3 1 1 1 3 )
  deg=2, size=9, uSize=5, minSpan=0.25, maxSpan=0.25
  
  Active basis functions on 0:
  3
  4
  5
  And their values:
  0
  0
  1
  

  And similarly here is an example of how to compute the Greville abscissae, determine the basis functions active on them, and compute their values.

  #include <gismo.h>
   
  using namespace gismo;
   
  int main(int, char**)
  {
      gsKnotVector<> kv (-1, 0, 3, 3, 1 );
      gsBSplineBasis<> basis(kv);
   
      gsMatrix<> greville  = basis.anchors();
      gsInfo << greville <<  "\n\n";
   
      gsMatrix<index_t> actmat;
      basis.active_into( greville, actmat );
      gsInfo << actmat <<  "\n\n";
   
      gsMatrix<> evaluate  = basis.eval( greville );
      gsInfo << evaluate <<  "\n\n";
   
      
   
      return 0;
  }

  Output:

      -1 -0.875 -0.625 -0.375 -0.125      0
      1  0.25 0.125 0.125 0.125     0
      0 0.625  0.75  0.75 0.625     0
      0 0.125 0.125 0.125  0.25     1
  

  Several basic operations are available: degree elevation, knot insertion, uniform refinement, interpolation, and so on, see bSplineBasis_example.cpp for a few of them.

Contrusction of a B-spline curve.

• gsBSpline This class derives from gsCurve and consists of a gsBSplineBasis plus a matrix which represents the coefficients in the basis. Therefore, the matrix contains the control points of the B-spline curve.

  Here is an example of how to create a B-spline curve, by declaring its basis and coefficients.

      // Make a BSpline curve
      gsKnotVector<> kv(0, 1, 1, 3);//start,end,interior knots, start/end multiplicites of knots
      gsMatrix<> coefs(4, 3);
      coefs << 0, 0, 0,
               1, 2, 3,
               2, 1, 4,
               4, 4, 4;
   
      gsBSpline<> curve(kv, coefs);

These B-spline related classes are implemented in the Nurbs module.

Multi-variate B-splines

The extantion to multi dimentional space is based on tensor-product constructions.

• gsTensorBSplineBasis<d>

  The tensor-product basis of dimension d where the coordinates are gsBSplineBasis. This class derives from gsBasis, representing a set of tensor-product B-spline basis functions.

  Here is an example how to construct a bivariate tensor product BSpline basis, compute the domain tesselations (meshes) and visualize these elements in paraview.

  #include <gismo.h>
   
  using namespace gismo;
   
  int main(int, char**)
  {
      gsKnotVector<>   ku (-1, 1, 3, 4); // fist, last, interior, multEnd
      gsKnotVector<>   kv (-1, 1, 1, 4); // fist, last, interior, multEnd
      
      gsTensorBSplineBasis<2> basis( ku, kv );
      
      gsMesh<> mesh(basis);
   
      gsWriteParaview( basis, "basis", 1000); // object, name, number of plotting samples
      gsWriteParaview( mesh, "mesh");
      return 0;
  }

  For additional properites and operations, e.g. basis size, basis support, evaluation, derivation, refinement, etc., see basis_example.cpp.

• gsTensorBSpline<d>

  A function defined by a gsTensorBSplineBasis plus a coefficient vector. As before, the number d stands for the dimension. For d=2 we have a gsSurface, for d=3 we have a gsVolume and for d=4 a gsBulk.

Similarly, gsNurbsBasis, gsNurbs, gsTensorNurbsBasis and gsTensorNurbs refer to Non-uniform rational B-spline bases patches (functions) of dimension one, or more, respectively.

Hierarchical B-splines

gsHBSplineBasis and gsTHBSplineBasis defines the hierarchical B-spline and the truncated hierarchical B-spline basis, respectively. Note that both are derived from gsHTensorBasis.

The corresponding geometric objects are gsHBSpline<d, T> and gsTHBSpline<d, T>, where d stands for the dimension and T templates the type.

thbSplineBasis_example.cpp contains a brief introduction and overview to gsTHBSplineBasis. Additional examples can be found in thbRefinement_example.cpp for standard refinement operations, as well as in gsHBox_example, and gsAdaptiveMeshing for admissible refinement and coarsening operations.

gsGeometry example

All parametric objects (curves, surfaces or volumes) derive from the class gsGeometry. geometry_example.cpp illustrates a more generic example to create an analysis any given geometric object.

Creating simple geometries

• The class gsNurbsCreator has several functions that allow us to create (compute) the B-spline basis and the control points of some standard geometries.

Re-constructing geometries

• The fitting_example.cpp shows how we can fit data points with B-splines.

Multi-patch

A gsMultiPatch object consists of a collection of patches with topological information. The topology is given by the boundaries and the adjacency graph, defining the connections between patches along boundaries.

Here is an XML file defining a simple 2-patch rectangle (two_patches.xml):

<?xml version="1.0" encoding="UTF-8"?>
<!--
This is a simple example of two squares, parametrized by linear 
B-splines meeting along one side
-->
<xml>
  <!-- Patch 0 -->
  <Geometry type="TensorBSpline2" id="0">
    <Basis type="TensorBSplineBasis2">
      <Basis type="BSplineBasis" index="0">
        <KnotVector degree="1">0 0 1 1 </KnotVector>
      </Basis>
      <Basis type="BSplineBasis" index="1">
        <KnotVector degree="1">0 0 1 1 </KnotVector>
      </Basis>
    </Basis>
    <coefs geoDim="2">
      0.0 0.0 
      1.0 0.0 
      0.0 1.0 
      1.0 1.0 
    </coefs>
  </Geometry>
 
  <!-- Patch 1 -->
  <Geometry type="TensorBSpline2" id="1">
    <Basis type="TensorBSplineBasis2">
      <Basis type="BSplineBasis" index="0">
        <KnotVector degree="1">0 0 1 1 </KnotVector>
      </Basis>
      <Basis type="BSplineBasis" index="1">
        <KnotVector degree="1">0 0 1 1 </KnotVector>
      </Basis>
    </Basis>
    <coefs geoDim="2">
      -1.0 0.0 
       0.0 0.0 
      -1.0 1.0 
       0.0 1.0 
    </coefs>
  </Geometry>
 
  <!-- A multipatch section describes the configuration
       of the two patches above -->
  <MultiPatch parDim="2" id="2">
    <patches type="id_range">0 1</patches>
    <interfaces>1 2 0 1 0 1 1 1
    </interfaces>
    <boundary>1 4
    1 3
    0 4
    0 3
    0 2
    1 1
    </boundary>
  </MultiPatch>
 
</xml>

The file contains the patches plus information on the boundaries and interfaces between them. A boundary is a side that does not meet with another side. An interface consists of two sides that meet plus orientation information. The following illustration describes the data:

Illustration of file two_patches.xml

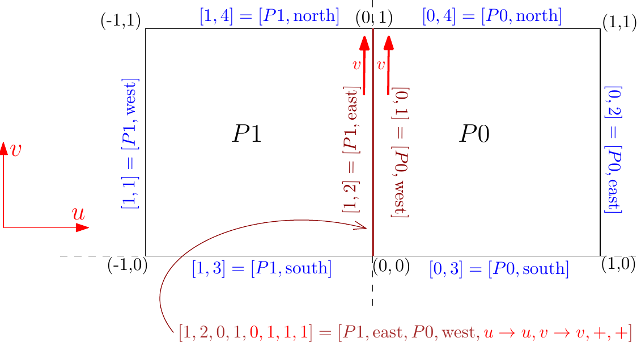
See also gismo::boundary and gismo::boundaryInterface for more information on the meaning of the multipatch data.

Analogously to multipatch objects, a gsMultiBasis object is a collection of gsBasis classes together with topological information such as boundaries and interfaces.